深度学习掀开了机器学习的新篇章,目前深度学习应用于图像和语音已经产生了突破性的研究进展。深度学习一直被人们推崇为一种类似于人脑结构的人工智能算法,那为什么深度学习在语义分析领域仍然没有实质性的进展呢?
引用三年前一位网友的话来讲:
“Steve Renals算了一下icassp录取文章题目中包含deep learning的数量,发现有44篇,而naacl则有0篇。有一种说法是,语言(词、句子、篇章等)属于人类认知过程中产生的高层认知抽象实体,而语音和图像属于较为底层的原始输入信号,所以后两者更适合做deep learning来学习特征。”
实际上,就目前而言,Deep Learning 在 NLP 领域中的研究已经将高深莫测的人类语言撕开了一层神秘的面纱。其中最有趣也是最基本的,就是“词向量”了。
1. 词向量
自然语言理解的问题要转化为机器学习的问题,第一步肯定是要找一种方法把这些符号数学化。
NLP 中最直观,也是到目前为止最常用的词表示方法是 One-hot Representation,这种方法把每个词表示为一个很长的向量。这个向量的维度是词表大小,其中绝大多数元素为 0,只有一个维度的值为 1,这个维度就代表了当前的词。 举个栗子, “话筒”表示为 [0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 …] “麦克”表示为 [0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 …] 每个词都是茫茫 0 海中的一个 1。 这种 One-hot Representation 如果采用稀疏方式存储,会是非常的简洁:也就是给每个词分配一个数字 ID。比如刚才的例子中,话筒记为 3,麦克记为 8(假设从 0 开始记)。如果要编程实现的话,用 Hash 表给每个词分配一个编号就可以了。这么简洁的表示方法配合上最大熵、SVM、CRF 等等算法已经很好地完成了 NLP 领域的各种主流任务。 当然这种表示方法也存在一个重要的问题就是“词汇鸿沟”现象:任意两个词之间都是孤立的。光从这两个向量中看不出两个词是否有关系,哪怕是话筒和麦克这样的同义词也不能幸免于难。此外,这种表示方法还容易发生维数灾难,尤其是在Deep Learning相关的一些应用中。2.Distributed representation词向量表示
既然上述这种易于理解的One-hot Representation词向量表示方式具有这样的重要缺陷,那么就需要一种既能表示词本身又可以考虑语义距离的词向量表示方法,这就是我们接下来要介绍的Distributed representation词向量表示方法。
Distributed representation 最早由 Hinton在 1986 年提出。它是一种低维实数向量,这种向量一般长成这个样子:
[0.792, −0.177, −0.107, 0.109, −0.542, …]
维度以 50 维和 100 维比较常见,当然了,这种向量的表示不是唯一的。
Distributed representation 最大的贡献就是让相关或者相似的词,在距离上更接近了(看到这里大家有没有想到普通hash以及simhash的区别呢?有兴趣的同学请见博客《》)。向量的距离可以用最传统的欧氏距离来衡量,也可以用 cos 夹角来衡量。用这种方式表示的向量,“麦克”和“话筒”的距离会远远小于“麦克”和“天气”。可能理想情况下“麦克”和“话筒”的表示应该是完全一样的,但是由于有些人会把英文名“迈克”也写成“麦克”,导致“麦克”一词带上了一些人名的语义,因此不会和“话筒”完全一致。将 word映射到一个新的空间中,并以多维的连续实数向量进行表示叫做“Word Represention” 或 “Word Embedding”。自从21世纪以来,人们逐渐从原始的词向量稀疏表示法过渡到现在的低维空间中的密集表示。用稀疏表示法在解决实际问题时经常会遇到维数灾难,并且语义信息无法表示,无法揭示word之间的潜在联系。而采用低维空间表示法,不但解决了维数灾难问题,并且挖掘了word之间的关联属性,从而提高了向量语义上的准确度。
3.词向量模型
a) LSA矩阵分解模型
采用线性代数中的奇异值分解方法,选取前几个比较大的奇异值所对应的特征向量将原矩阵映射到低维空间中,从而达到词矢量的目的。
b) PLSA 潜在语义分析概率模型
从概率学的角度重新审视了矩阵分解模型,并得到一个从统计,概率角度上推导出来的和LSA相当的词矢量模型。
c) LDA 文档生成模型
按照文档生成的过程,使用贝叶斯估计统计学方法,将文档用多个主题来表示。LDA不只解决了同义词的问题,还解决了一次多义的问题。目前训练LDA模型的方法有原始论文中的基于EM和 差分贝叶斯方法以及后来出现的Gibbs Samplings 采样算法。
d) Word2Vector 模型
最近几年刚刚火起来的算法,通过神经网络机器学习算法来训练N-gram 语言模型,并在训练过程中求出word所对应的vector的方法。本文将详细阐述此方法的原理。
4.word2vec算法思想
什么是word2vec?你可以理解为word2vec就是将词表征为实数值向量的一种高效的算法模型,其利用深度学习的思想,可以通过训练,把对文本内容的处理简化为 K 维向量空间中的向量运算,而向量空间上的相似度可以用来表示文本语义上的相似。
Word2vec输出的词向量可以被用来做很多 NLP 相关的工作,比如聚类、找同义词、词性分析等等。如果换个思路, 把词当做特征,那么Word2vec就可以把特征映射到 K 维向量空间,可以为文本数据寻求更加深层次的特征表示 。
Word2vec 使用的词向量不是我们上述提到的One-hot Representation那种词向量,而是 Distributed representation 的词向量表示方式。其基本思想是 通过训练将每个词映射成 K 维实数向量(K 一般为模型中的超参数),通过词之间的距离(比如 cosine 相似度、欧氏距离等)来判断它们之间的语义相似度.其采用一个 三层的神经网络 ,输入层-隐层-输出层。有个核心的技术是 根据词频用Huffman编码 ,使得所有词频相似的词隐藏层激活的内容基本一致,出现频率越高的词语,他们激活的隐藏层数目越少,这样有效的降低了计算的复杂度。而Word2vec大受欢迎的一个原因正是其高效性,Mikolov 在论文中指出,一个优化的单机版本一天可训练上千亿词。
这个三层神经网络本身是 对语言模型进行建模 ,但也同时 获得一种单词在向量空间上的表示 ,而这个副作用才是Word2vec的真正目标。
与潜在语义分析(Latent Semantic Index, LSI)、潜在狄立克雷分配(Latent Dirichlet Allocation,LDA)的经典过程相比,Word2vec利用了词的上下文,语义信息更加地丰富。
Word2Vec实际上是两种不同的方法:Continuous Bag of Words (CBOW) 和 Skip-gram。CBOW的目标是根据上下文来预测当前词语的概率。Skip-gram刚好相反:根据当前词语来预测上下文的概率(如下图所示)。这两种方法都利用人工神经网络作为它们的分类算法。起初,每个单词都是一个随机 N 维向量。经过训练之后,该算法利用 CBOW 或者 Skip-gram 的方法获得了每个单词的最优向量。
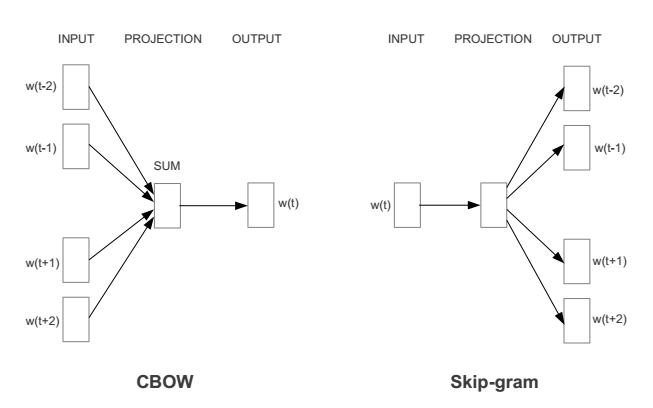
取一个适当大小的窗口当做语境,输入层读入窗口内的词,将它们的向量(K维,初始随机)加和在一起,形成隐藏层K个节点。输出层是一个巨大的二叉 树,叶节点代表语料里所有的词(语料含有V个独立的词,则二叉树有|V|个叶节点)。而这整颗二叉树构建的算法就是Huffman树。这样,对于叶节点的 每一个词,就会有一个全局唯一的编码,形如"010011",不妨记左子树为1,右子树为0。接下来,隐层的每一个节点都会跟二叉树的内节点有连边,于是 对于二叉树的每一个内节点都会有K条连边,每条边上也会有权值。
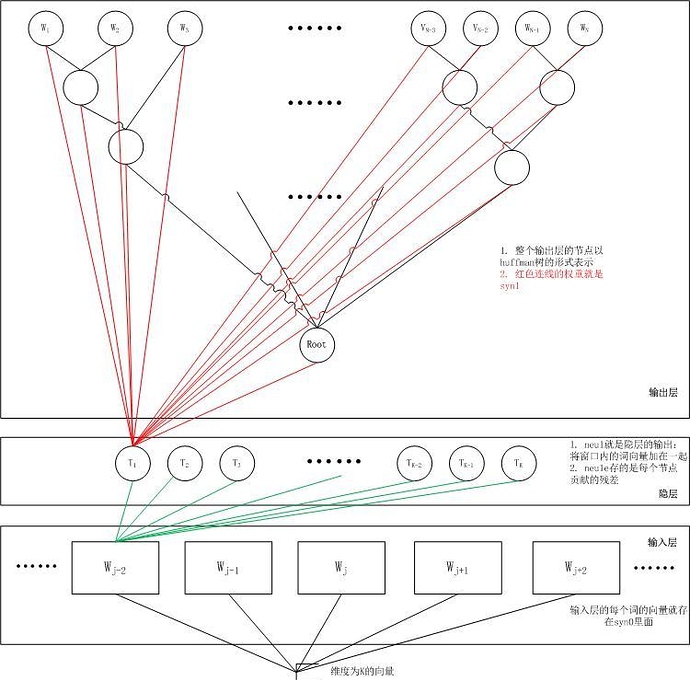
对于语料库中的某个词w_t,对应着二叉树的某个叶子节点,因此它必然有一个二进制编码,如"010011"。在训练阶段,当给定上下文,要预测后 面的词w_t的时候,我们就从二叉树的根节点开始遍历,这里的目标就是预测这个词的二进制编号的每一位。即对于给定的上下文,我们的目标是使得预测词的二 进制编码概率最大。形象地说,我们希望在根节点,词向量和与根节点相连经过 logistic 计算得到 bit=1 的概率尽量接近 0,在第二层,希望其 bit=1 的概率尽量接近1,这么一直下去,我们把一路上计算得到的概率相乘,即得到目标词w_t在当前网络下的概率P(w_t),那么对于当前这个 sample的残差就是1-P(w_t),于是就可以使用梯度下降法训练这个网络得到所有的参数值了。显而易见,按照目标词的二进制编码计算到最后的概率 值就是归一化的。
Hierarchical Softmax用Huffman编码构造二叉树,其实借助了分类问题中,使用一连串二分类近似多分类的思想。例如我们是把所有的词都作为输出,那么“桔 子”、“汽车”都是混在一起。给定w_t的上下文,先让模型判断w_t是不是名词,再判断是不是食物名,再判断是不是水果,再判断是不是“桔子”。
但是在训练过程中,模型会赋予这些抽象的中间结点一个合适的向量,这个向量代表了它对应的所有子结点。因为真正的单词公用了这些抽象结点的向量,所 以Hierarchical Softmax方法和原始问题并不是等价的,但是这种近似并不会显著带来性能上的损失同时又使得模型的求解规模显著上升。
没有使用这种二叉树,而是直接从隐层直接计算每一个输出的概率——即传统的Softmax,就需要对|V|中的每一个词都算一遍,这个过程时间复杂 度是O(|V|)的。而使用了二叉树(如Word2vec中的Huffman树),其时间复杂度就降到了O(log2(|V|)),速度大大地加快了。
现在这些词向量已经捕捉到上下文的信息。我们可以利用基本代数公式来发现单词之间的关系(比如,“国王”-“男人”+“女人”=“王后”)。这些词向量可 以代替词袋用来预测未知数据的情感状况。该模型的优点在于不仅考虑了语境信息还压缩了数据规模(通常情况下,词汇量规模大约在300个单词左右而不是之前 模型的100000个单词)。因为神经网络可以替我们提取出这些特征的信息,所以我们仅需要做很少的手动工作。但是由于文本的长度各异,我们可能需要利用 所有词向量的平均值作为分类算法的输入值,从而对整个文本文档进行分类处理。
5.doc2vec算法思想
然而,即使上述模型对词向量进行平均处理,我们仍然忽略了单词之间的排列顺序对情感分析的影响。即上述的word2vec只是基于词的维度进行"语义分析"的,而并不具有上下文的"语义分析"能力。
作为一个处理可变长度文本的总结性方法,Quoc Le 和 Tomas Mikolov 提出了 Doc2Vec方法。除了增加一个段落向量以外,这个方法几乎等同于 Word2Vec。和 Word2Vec 一样,该模型也存在两种方法:Distributed Memory(DM) 和 Distributed Bag of Words(DBOW)。DM 试图在给定上下文和段落向量的情况下预测单词的概率。在一个句子或者文档的训练过程中,段落 ID 保持不变,共享着同一个段落向量。DBOW 则在仅给定段落向量的情况下预测段落中一组随机单词的概率。
以下内容摘自
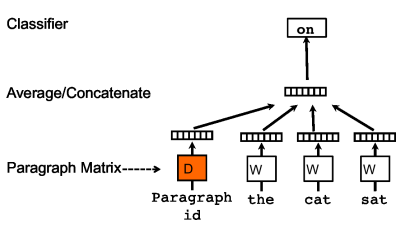
先看c-bow方法,相比于word2vec的c-bow模型,区别点有:
- 训练过程中新增了paragraph id,即训练语料中每个句子都有一个唯一的id。paragraph id和普通的word一样,也是先映射成一个向量,即paragraph vector。paragraph vector与word vector的维数虽一样,但是来自于两个不同的向量空间。在之后的计算里,paragraph vector和word vector累加或者连接起来,作为输出层softmax的输入。在一个句子或者文档的训练过程中,paragraph id保持不变,共享着同一个paragraph vector,相当于每次在预测单词的概率时,都利用了整个句子的语义。
- 在预测阶段,给待预测的句子新分配一个paragraph id,词向量和输出层softmax的参数保持训练阶段得到的参数不变,重新利用梯度下降训练待预测的句子。待收敛后,即得到待预测句子的paragraph vector。
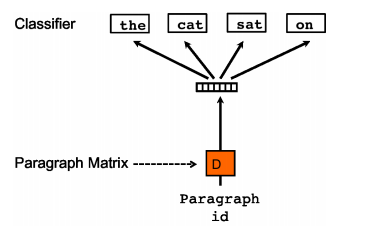
sentence2vec相比于word2vec的skip-gram模型,区别点为:在sentence2vec里,输入都是paragraph vector,输出是该paragraph中随机抽样的词。
下面是sentence2vec的结果示例。先利用中文sentence语料训练句向量,然后通过计算句向量之间的cosine值,得到最相似的句子。可以看到句向量在对句子的语义表征上还是相当惊叹的。

6.参考内容
1. word2vec官方地址:
2. python版本word2vec实现:
3. python版本doc2vec实现:
4.
5. 练数成金:
6.